Un altro tipo di matematica

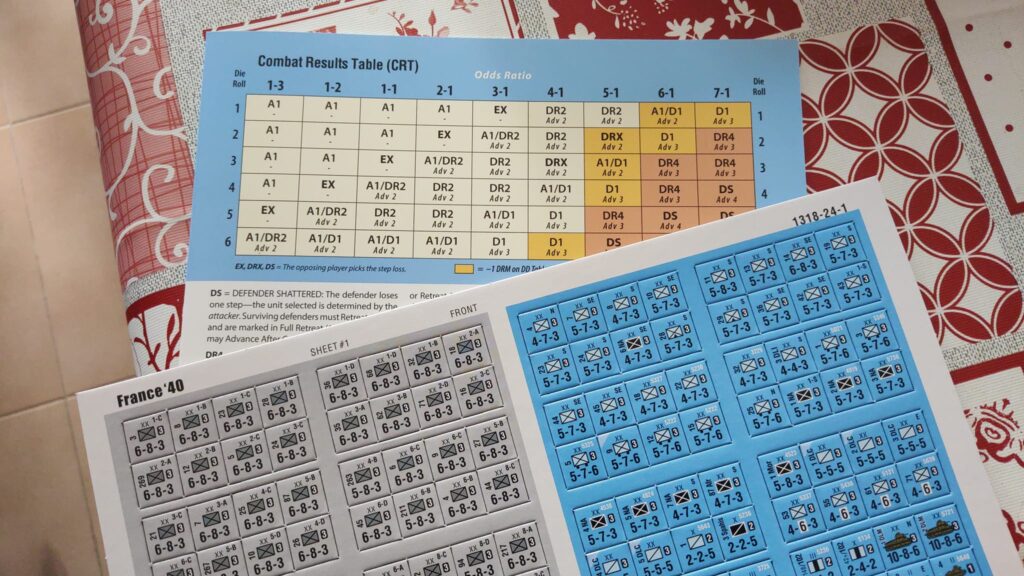
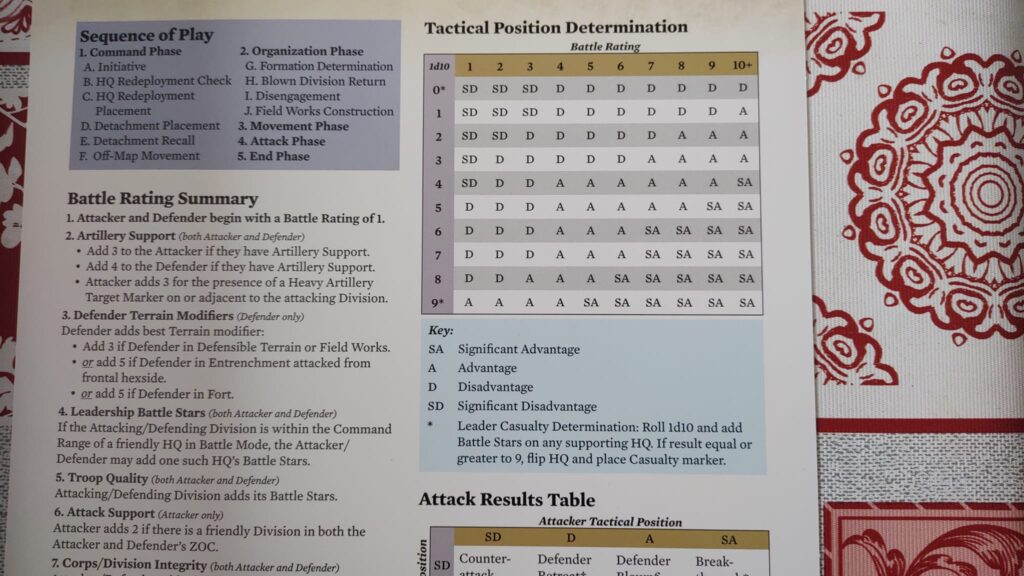
Che cosa costituisce realmente un gioco di simulazione? I suoi componenti, mi direte. Mappe, pedine, carte, tabelle, dadi… Eh, sì, ma quelli sono solo elementi esteriori, delle “materializzazioni” di qualcosa di più profondo e sottile. La riprova è che se usassimo un altro materiale per creare la stessa mappa, un pacchetto di grafiche alternative per realizzare le stesse pedine, un set di dadi speciali per ottenere le stesse probabilità di una tabella non cambierebbe assolutamente nulla ai fini del gioco. E in effetti questo è proprio ciò che succede con le mappe deluxe plastificate o in cartoncino che si possono acquistare separatamente per un gioco che ne ha già una in carta semplice, o con i print and play che puoi realizzare in modalità differenti rispetto a quelle originariamente previste (vedetevi i miei video su Horse & Musket e capirete subito), o con i dadi con simboli appositi presenti in Annibale e Amilcare e in Warfare della WBS, o infine con i giochi della Dissimula che vi fanno scegliere tra pedine con simboli NATO oppure con silhouette e uniformi.

Insomma, questi componenti (quale che sia la loro forma o materiale di realizzazione) sono meri strumenti di quelle componenti fisse che stanno alla base del gioco: valori prestabiliti, combinazioni, probabilità, rappresentazioni topografiche, mappe concettuali… questa roba qui.

E che cosa “tiene insieme” realmente un gioco di simulazione? Tutte quelle funzioni e relazioni che fanno interagire tra di loro gli elementi di prima. Le zone di controllo determinano gli effetti reciproci della prossimità. Le tabelle di combattimento ricostruiscono l’interazione delle unità che si scontrano. Le manipolazioni dei mazzi di carte rappresentano le variazioni nella probabilità del verificarsi di determinati eventi.

Tutto questo ha un nome, che forse a sentirlo fa un po’ paura ad alcuni, ma che in realtà è molto bello e meno complesso di quanto sembri: matematica. Da qui le equazioni rappresentative di tutti questi fattori che si muovono una accanto all’altra ad ogni nostra mossa, che entrano in contatto tra di loro ad ogni azione e reazione, che si vanno ad inserire in processi predeterminati componendo – segmento dopo segmento, fase dopo fase, turno dopo turno – quelli che potremmo definire gli algoritmi della simulazione stessa. Ben lo avevano capito, lo abbiamo ripetuto molte volte, matematici come von Neumann e Nash, inventori rispettivamente dell’esagono e del segnalino alla RAND Corporation: per gli amici, hex and counter.

Solo che nel caso del gioco di simulazione, questa non è la disciplina che abbiamo studiato a scuola, o meglio, non solo. Perché parliamo di gioco di simulazione, e nel termine “gioco” vivono due elementi fondamentali: la libertà di giocare (grazie, caro nonno Huizinga) e l’interazione tra più soggetti e i rispettivi processi decisionali. Anche nei solitari, con l’unica distinzione che lì uno dei soggetti è “automatizzato” in vario modo.

Libera interazione. Determinata però anch’essa da regole, molto precise, note a entrambi i giocatori e accettate da tutti (quindi, anche modificabili di comune accordo). Equazioni, algoritmi e libera interazione insieme, a comporre quello che ho a più riprese definito “un altro tipo di matematica”.

Una matematica che nel gioco non è solo numerica e funzionale, ma anche profondamente umana. Quindi, non lineare, non del tutto prevedibile, non riducibile solo ai numeri e numeretti di pedine e tabelle, non interamente razionale come ci insegnano le scienze comportamentali, con i loro bias cognitivi, le distorsioni decisionali, le tecniche di nudge, l’importanza della psicologia e tutto il resto.

Niente di tutto ciò è un caso.

Il grande filosofo e matematico Leibniz, in una lettera ad un amico, ipotizzava la possibilità di creare un gioco “per capitani e generali” che permettesse, tramite un’accorta ponderazione delle possibilità statistiche sulla base di osservazioni scientifiche e topografiche, di ricreare dei fatti d’arme su di un tavolo, magari con una mappa e delle pedine. Se avesse dato seguito a questa intuizione, il wargame come lo conosciamo noi e di lì il gioco di simulazione moderno sarebbero nati forse con un buon secolo di anticipo rispetto al Kriegsspiel ottocentesco.

Ma prima ancora di Leibniz e delle sue missive, un altro pensatore già aveva postulato che si poteva scoprire di più sul carattere di una persona in un’ora di gioco che in un anno di conversazione: Platone. E lui ben lo sapeva, estimatore com’era di quella petteia o “gioco dei fanti” giocata su di un tabellone ortogonale, alla quale aveva fatto appassionare anche l’allievo Aristotele (il quale avrebbe tramandato il gusto per lo stesso gioco al suo allievo, Alessandro Magno… che lo avrebbe giocato in versione “live” sui campi di battaglia di mezzo mondo).

Dunque, se Leibniz ci aiuta a comprendere l’aspetto oggettivo della simulazione (gli intrecci numerico-statistici e le loro funzioni), Platone vi unisce l’elemento umano e concettuale (gli aspetti psicologico-cognitivi, sublimati nelle relazioni interpersonali). Due forme di matematica che dialogano insieme e si confrontano, diventando profondamente creative.

Da qui, Platone e le sue indagini sul mondo delle idee ci portano ad un’altra forma di matematica ancora, forse quella più conosciuta e al tempo stesso “nascosta”, ossia la musica. Le melodie, gli accordi, le risonanze… i musicisti lo sanno bene, sono tutte relazioni matematiche ben precise e cadenzate. E creano mondi.

Ma questa è ancora tutta un’altra tipologia di matematica, di cui parleremo in una prossima occasione.